§15　因果の旅に出かけよう

因果〔原因→結果〕は使えます。
原因をいじれば、結果が変わるん
ですから。困ったときの因果！と
言われる位、頼りにされます。
　　　　　（ちょっと盛りました）

この因果、得意にしましょう！

複雑なアクション・プランを描く
ときにも有効です。（§14参照）

ということで、さっそく。
因果、トリセツします。

それでは　関係の話から

因果を理解するには、
まず因果を関係として意識する
必要があります。

なので、急がば回れ！的に
因果の前に、関係の話を。

関係って、ＡとＢのつながりです。
人と人のつながり、人間関係。

こんなつながりの中に
共変関係という
タイプがあります。共変関係って
「こちらが変わると、あちらが
変わる。その逆もあり」な関係。

たとえば、

練習すると上達する
　は共変関係。

上達すると練習する
　も共変関係。

分からなくなった？


それは、あなたが
無意識に先へ進んでいるから！
気にしないで先へ進みましょう。

では、これは？

練習するから上達する

上達するから練習する

前との違いは「から」。
「と」が「から」に変わりました。
すると、共変関係は…

因果関係になります

原因から結果、からを→で表すと
原因→結果。これが因果関係。

どちらが原因でどちらが結果？　が
はっきりしない共変関係の中で
原因と結果が確定した特殊な関係を
因果関係と呼ぶのです。

わかった？　 いい感じです。

さらにレベルアップしましょう！

因果関係の納得度

練習する→上達する
上達する→練習する
（「から」を→で表現。以下、同じ）

これら２つは因果関係ですが、
納得度は同じでしょうか？

練習する→上達するは
スポーツや楽器の演奏などを
考えると、納得度は高そう。

では、
上達する→練習するは？

人って、上達を確認しただけで
練習するでしょうか？

上達する→嬉しい→練習する　の
ほうが納得がいく気がしませんか。

もし、そうだとすれば、これは…

最初の　原因→結果の 結果 が
次の　　原因→結果の 原因 になり、
最後に　結果（＝練習する）を生む、

ちょっと複雑な因果関係なのかも？

こんな風に納得度に注意できると
因果関係の構造が見えてくるように
なるのです。

というわけで　因果関係いろいろ

因果関係の基本構造は
原因→結果（練習する→上達する）

ですが、さきほどの例のような
原因→　結果（転じて原因）→結果
（上達する→嬉しい→練習する）
もあります。

複数の原因（A,B,…）→１つの結果
そして、その逆の

１つの原因→複数の結果（A,B,…）
もあります。

つまり、原因となる事柄と
結果となる事柄は、→　によって
縦横無尽に結ばれているわけです。

この事をイメージできると
因果を描くが自由自在。

以下のように表すことも。

　　　　　

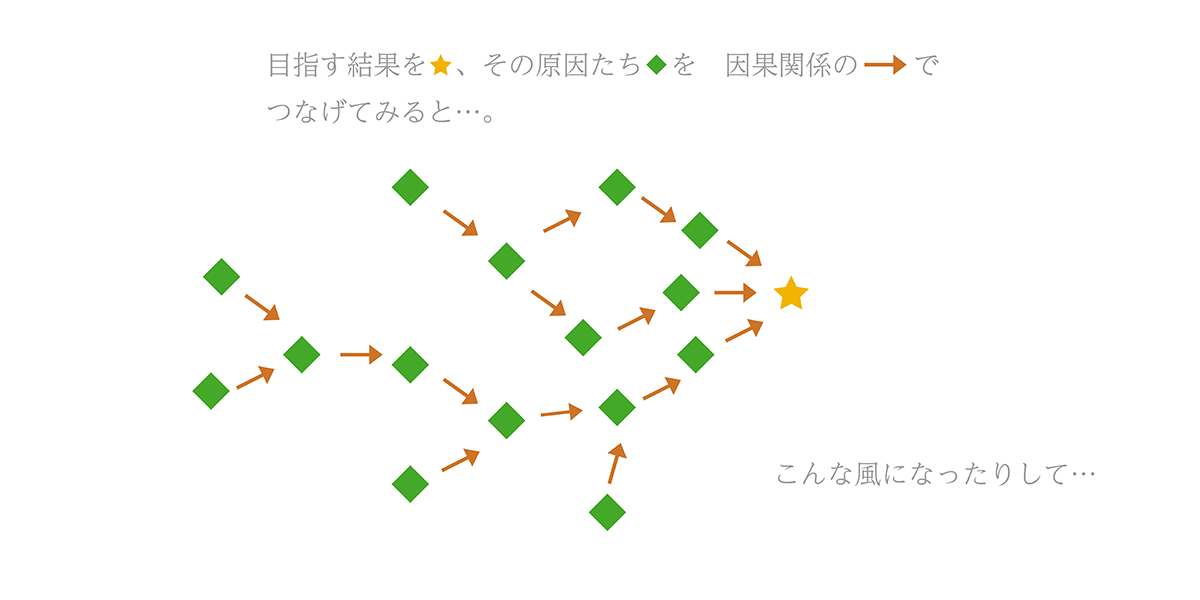
この図では、◆が原因、★が最終結
果、そして → が因果関係を表して
います。なんか面白そうでしょ。

こんな複雑な因果関係、あなたも
どんどん描いてみてください。

描けると　アクション・プランを

因果関係で描けるようになります。

§14（参照）で解説した通り、
アクション・プランの基本型は

海外で働きたいから+外国語を勉強
　　　〔理想〕　　+　〔行動〕

です。この基本型の
〔理想〕+〔行動〕って、因果関係に
書き直すことができます。

〔理想〕が因果の最終結果、
〔行動〕は最終結果を導く原因。

そう考えることで、
アクション・プランを
因果関係の図として描き直すことが
できるんです。この例なら、

外国語を勉強する → 海外で働ける
　　〔行動〕　　 → 　〔理想〕
　　〔原因〕　　 → 　〔結果〕

と書き直すことができます。

すると自然に、
アクション・プランの精度が
上がり始めます。

なぜか？

あなたは気づいちゃうんです。
「外国語を勉強する」のほかに
原因がありそうなことに。

たとえば、
「外資系企業に就職する」
「就労ビザを取得する」
「外国の市民権を得る」など
複数の原因を想定し、

外国語を勉強する →海外で働ける
外資系企業に就職する →海外で働ける
就労ビザを取得する →海外で働ける
外国の市民権を得る →海外で働ける

な因果関係を想い描きます。

そして、複数の原因の中でどれが
アイデアとして望ましく実行可能か
の検討を始めるでしょう。

同時に、
今のアイデアに足りない部分、
考案したアクション・プランの
弱いところを痛感するはずです。

ですから修正。
すると確かさらしさがアップ。
プランの成功率は高くなります。

わかっちゃった？　楽勝？
さすが！　すごい！

ここまで理解したあなた は
きっと次の点が気になるでしょう。

「その因果関係、必ず？」

とても良い指摘です。
結果に殆ど貢献しない原因は
どうでもいいんですから。

では、この問題に
どう対処したらよいのでしょう？
糸口として、
因果関係の確からしさの度合い、
確度の話を書きます。

その因果関係、必ず？

確からしさの度合いを
確度と言います。

確度には、おおまかなランクが
あって、因果関係を分類すると、
以下のランクに分かれます。

確度が最も高い因果関係は…
100％保証です。

この因果は、理論theory、法則law
なんて呼ばれます。Ａが変われば
必ずＢも変わります。例外なし。公
式（速度×時間＝距離）と同じ水準。
この確度を、科学（例　物理学）は
探します。すべての発見は世界中で
再確認（：再現）が絶対要件です。


次に確度が高い因果関係は、
確実に影響クラスに分類されます。

この因果は、論理logic とか、モデ
ルmodel とか呼ばれます。その確
度、100％保証まで行きませんが
確実に強い影響を及ぼすので、人の
心理や行動、社会変動の原因解明は
これで大成功というレベルです。

実は、ここまでが因果関係を数式で
表せる（：表すことに意味のある）
レベル。なので、〔結果Y〕は
〔原因X〕がａの強さで影響して、
誤差は e くらいだったとすると
「 Y=ａX+e で表そうよ」な話が
飛び交います。式の ＝ が確度の
高さを予感させるでしょ。

でも、もし確度がそれ以下だと…
影響するかも…へ降格

この因果はかなり脆弱。ありそうで
無かったり。ナンカ頼りなさ気。
「まぁ、あるかもね…」な扱いを
受けてしまう因果なのです。

確度としては「あらら」な因果で
すが、実際は、かなりオモシロ。
世の凄いアイデアは、こんな脆弱な
因果から。「そんなバカな…」が
素晴らしい結果を生み出すんです。

※たとえば、ヴィレバンやドンキ。
　ごちゃごちゃ陳列→オモシロイ　が
　小売業界の常識を変えました。

てな感じで、因果関係の確度は様々
です。違いを意識できると…

※この３段階で区分してください。因果
　関係の図を描くとき確度によって矢印
　の色を → → → と変えるのもいいか
　もしれません。

アイデアとして、アクション・プラ
ンとして、どの因果に注目すべき？
が見えてくるようになります。

納得したら　因果の旅へ！

ちょっと？？？な因果の話、
いかがでしたか？

難しそうで、遠回しな理屈のように
感じるかもしれませんが、単純で、
便利。どんどん使ってください。

新しい発見も増えますよ。

「激辛が人気。その原因は？」
「デカ盛りと原因は同じ？」
「あぁ、因果関係って！」

な推理推論が自然とできるように
なるんです。

ですから、因果の旅へ。

街を歩き、人々を観察し、my
世の中に隠れ潜んでいる因果関係を
たくさん見つけてください。

（おしまい）